관찰구간이 미지수로 제공되며, 해당 구간을 이동시키면서 최댓값, 최솟값 함수를 결정하는 문항은 최근 몇 년간 내신, 모의고사 단골 킬러 주제이다.

해당 주제는 공통수학1 이차함수에서 처음 등장하여, 추후 미적분1, 2에서도 출제되는 주제인 만큼 반드시 정복해야 하며 정확한 원리와 흐름을 이해하는 것을 목표로 꼼꼼하게 학습해야 한다. 해당 유형의 예시 문항을 살펴보자.

위와 같이, x가 아닌 t가 변함에 따라 관찰해야 하는 최댓값 함수, 최솟값 함수를 해석할 때는 크게 다음의 두 가지 풀이로 나누어진다.

두 가지 풀이 중, 평행 이동된 그래프를 활용한 두 번째 풀이가 훨씬 더 편하고 빠르지만, 만약 서술형에서 해당 문항이 출제될 경우, 구간을 나눠서 케이스 분류 후 문제를 푸는 것이 출제 의도이기에 반드시 두 가지 풀이를 모두 익히는 것을 추천한다. 수식적 풀이부터 살펴보자.

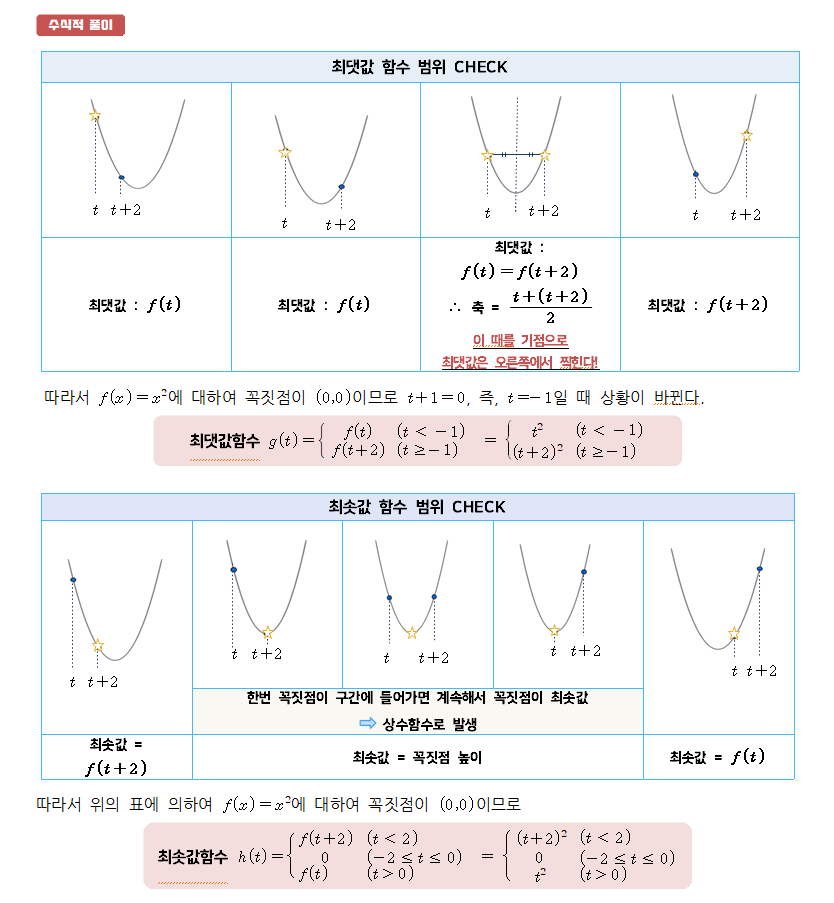
위와 같이 우선 이차함수의 축을 경계로 해당 관찰 구간이 축 기준 왼쪽에 있을 때, 축을 포함할 때, 축 오른쪽에 있을 때 따라서 크게 세 가지로 케이스 분류한다. 이후 관찰 구간이 축을 포함하는 케이스 내부에서 관찰 구간의 양 끝 중 어느 쪽이 축이랑 더 가까운지까지 고려하여 세부 케이스 분류를 진행하면 만족하는 함수를 찾아낼 수 있다.

위의 그림을 확인하며 머릿속에 이미지화하여 풀어나가는 것이 중요하다. 다소 복잡한 풀이이기에 충분한 시간을 확보한 후 꼼꼼하게 식을 정리해 나가는 것이 중요하며, 스스로 문제를 풀 때에도 반드시 여러 가지 그래프를 그려가며 푸는 것을 추천한다.

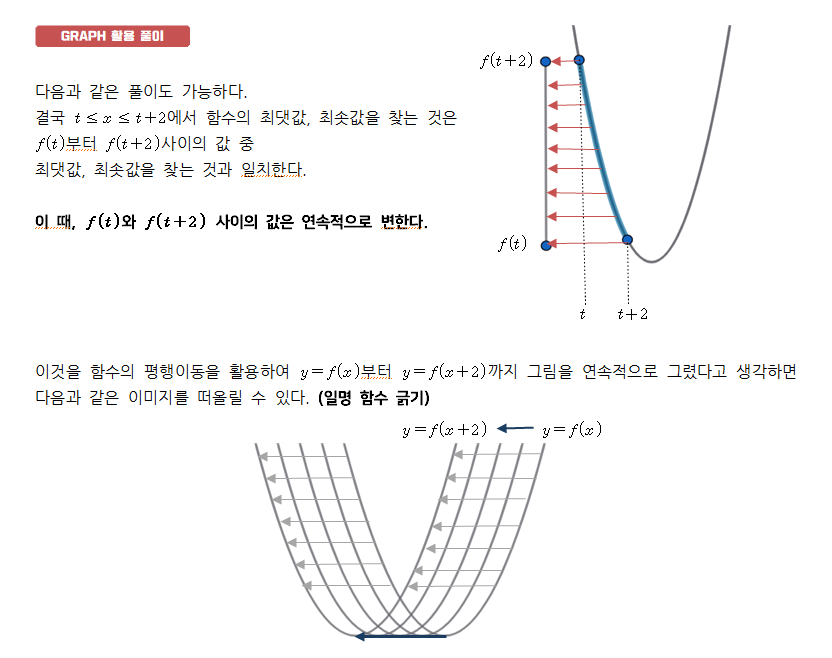
다음으로 사용할 수 있는 풀이법은 그래프의 평행이동을 활용한 풀이, 일명 ‘함수 긁기’를 활용한 풀이 스킬이다. 다만 이 풀이의 경우 어느 정도 공통수학1, 2 공부가 깊게 되어있는 학생들에게 좀 더 유리한 풀이이므로, 만약 본인이 공통수학1, 2를 여러 회독 공부한 상황이 아니라면 이전 첫 번째 풀이 위주로 학습하는 것을 추천한다.

위와 같은 두 가지 풀이법을 활용한 후 문제에서 제공된 여러 가지 추가 조건(예를 들어 직선과의 위치 관계 또는 실근 합)까지 해석하면 최종적으로 킬러문항을 풀어낼 수 있게 된다.

추후 미적분1에 가서는 해당 최댓값 함수 또는 최솟값 함수의 미분가능성 등을 물어보기도 하므로 개형까지 반드시 익혀두자. 

[추천]

전국 여러 학군지에서 다수의 학교가 자주 출제하는 킬러 주제인 만큼 반드시 해당 킬러 주제를 완벽히 마스터하자. 서술형을 염두에 둔 첫 번째 풀이도 자기 손으로 써낼 수 있도록 반드시 반복 훈련하는 것을 추천한다.