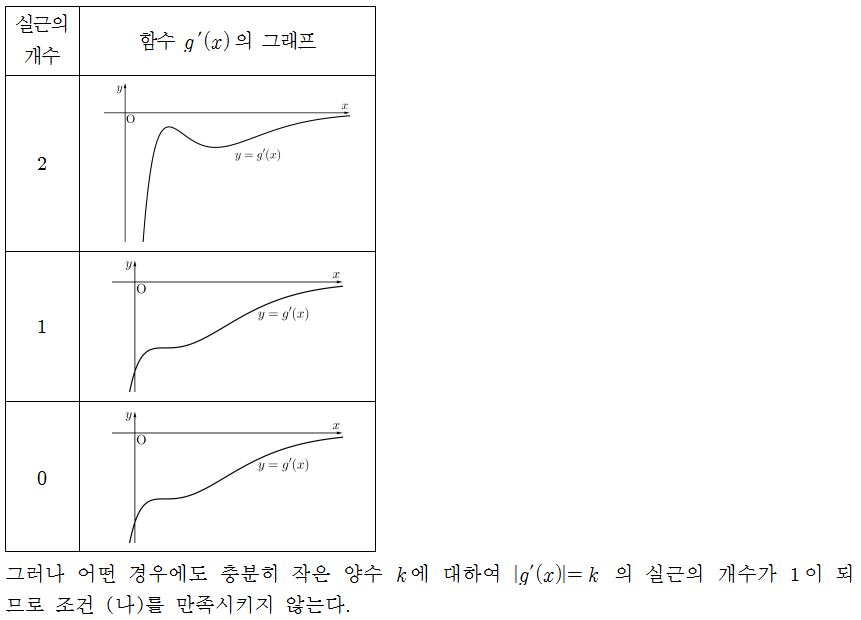
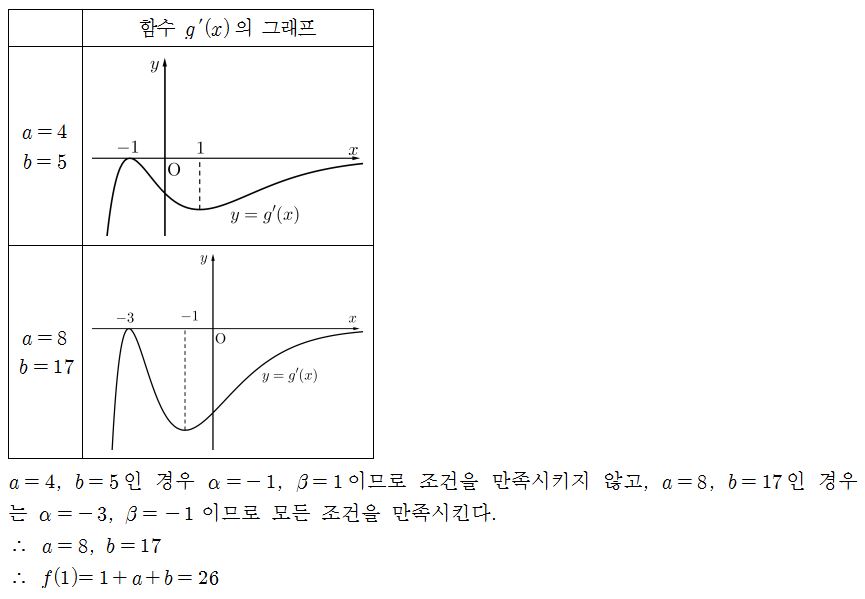
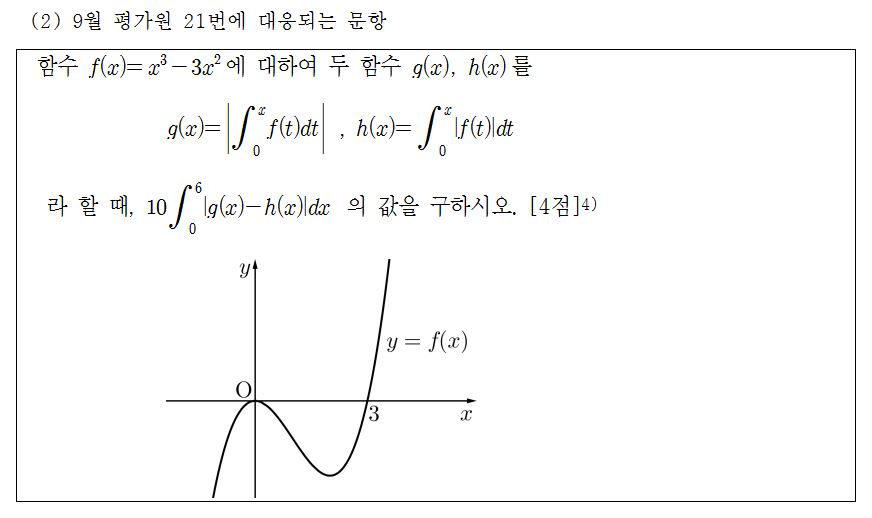
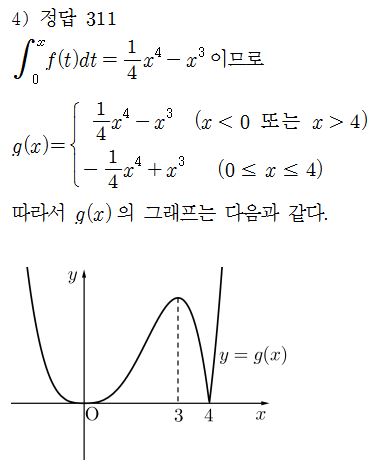
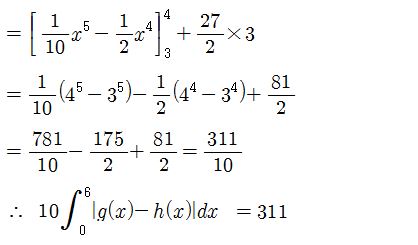정상모 스카이에듀 수학강사는 지난 6월 모의평가 수학 가형의 킬러문항으로 30번 ‘적분’ 문항을 꼽았다. 미지의 함수를 조건을 이용해 확정하는 복잡한 형태다. 특정 구간 내에서 함수를 구할 때 단순히 적분·미분하는 작업만으로 문제를 풀 수 없다. 원래 식과 미분한 식에 ㈎의 우함수 조건을 사용할 수 있도록 적당한 ?값을 대입하고 다시 조건에 미지수가 포함된 함수를 대입해 계산하는 단계를 통해 세 개의 식을 도출해 세 개의 미지수를 구해야 한다. 적분은 수학 가형에서 꾸준히 킬러문항으로 출제돼 왔다. 최근에는 독창적인 문제풀이의 아이디어를 요구하기보다 길고 복잡하더라도 차분하게 답을 도출할 수 있는 계산력을 평가하는 유형이 두드러지게 출제되고 있다<유사 문제 참조>.

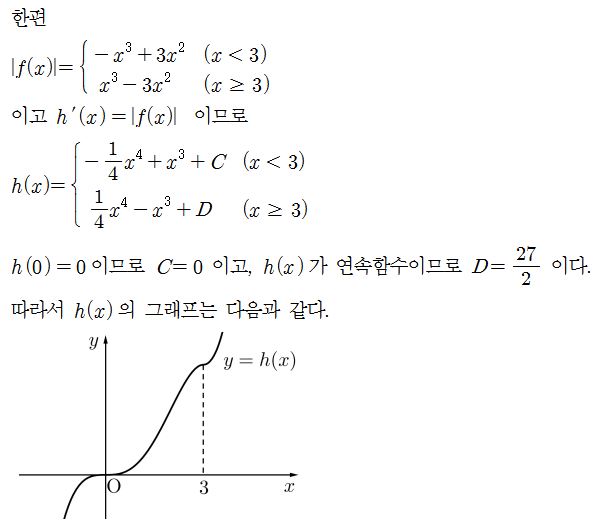
9월 모의평가에서는 절댓값을 포함한 함수의 미분 가능성을 묻는 30번 문항이 가장 오답률이 높았다. 조건을 이용해 함수의 구간을 나눠 사차함수를 확정하기 때문에 계산 과정이 간단하지 않다. 합성함수의 미분, 곱의 미분, 이계도함수 등이 문제풀이에 사용되지만 가장 중요한 개념은 절댓값함수를 ‘구간별로 정의된 함수’로 정리하고 그래프의 개형을 확인하는 것이다. 수렴하는 함수와 발산하는 함수를 곱한 결과가 수렴하려면 곱하는 수렴함수의 수렴값이 0이 돼야 하는 점도 알아야 한다. 도형의 방정식, 함수의 곱의 극한(미적분) 등 간접 출제범위에서 다루는 내용을 알아야 하기 때문에 고교 수학을 전반적으로 이해해야 한다. 절댓값을 포함한 함수의 미분 가능성 문항은 객관식으로도 출제될 수 있기 때문에 간접 출제범위의 내용이더라도 해당 개념을 복습하는 게 좋다.

수학 나형에서는 6월 모의평가 중 30번 문항이 ‘로그로 표현된 조건을 만족시키는 자연수 ?의 개수 세기’ 문항이 킬러 문항이었다. 개정 전 교육과정에 자주 출제됐던 문항으로 현 고 3 학생들에게 생소할 수 있는 문항이다. 로그에 대한 심도 있는 이해를 통해 문제를 해결하기보다 주어진 조건을 정리해 상황을 파악하고 차분히 개수를 세는 능력이 필요하다. 문자가 여러 개이기 때문에 식을 최대한 간단하게 정리해 기준을 잡아 개수를 세야 한다. 자연수의 조건을 이용해 1부터 차례대로 대입해 범위 내 ?의 값을 찾으면 된다. 표를 그리면 일목요연하게 정리하는 데 도움이 된다.

9월 모의평가에서는 ‘절댓값함수의 미분 가능성’을 묻는 21번 문항이 가장 난도가 높았다. 절댓값함수와 사차함수를 비교해 더 작은 부분을 함수로 설정한 뒤 해당 함수가 전 구간에서 미분 가능한지를 묻는 복잡한 문항이다. 다항함수의 절댓값함수 개형을 이해하는 것은 문제 해결에 필수적이다. 또한 절댓값함수를 이용해 미분계수의 크기를 조정할 수도 있고, 절댓값과 관련된 정적분 문항이 출제될 수도 있다.

[6·9월 모평 과목별 '킬러문항' 분석과 공략법 - 국어편]
[6·9월 모평 과목별 '킬러문항' 분석과 공략법 - 영어편]