이벤트

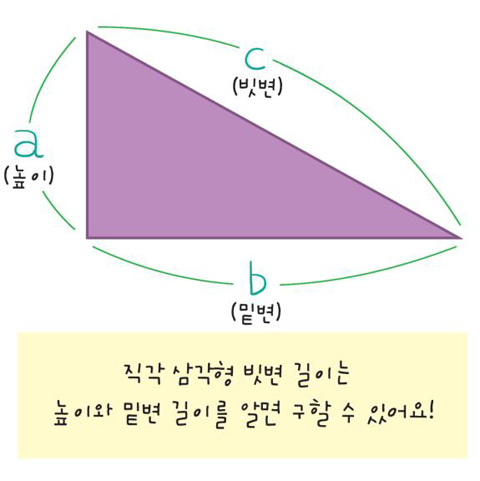
직각 삼각형의 빗변의 길이를 구하면 돼요

자, 이제 그 비밀을 같이 풀어봅시다. 건물 옥상과 바닥, 그리고 만국기를 연결할 운동장 바닥을 선으로 각각 연결해봐요. 그랬더니 어떤 도형이 생기나요? 그렇죠! 평소에 교과서에서 자주 보던 직각 삼각형이 만들어졌네요.

건물 바닥과 운동장 끝을 연결한 선은 직각 삼각형의 '밑변'이 됐고, 건물 바닥에서 옥상까지는 '높이', 옥상에서 운동장 바닥 끝까지 늘어뜨린 만국기는 '빗변'이 됐어요. 여기서 잠깐! 앞으로 직각 삼각형 하면 바로 떠오르게 될 유명한 수학 공식이 있어요. 고대 그리스의 수학자 피타고라스가 처음으로 증명했다는 이것은 무슨 공식일까요? 바로 직각 삼각형에서 빗변의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다는 '피타고라스의 정리'이지요(제곱은 두 번 곱하는 것을 뜻해요). 그럼 일단 길이의 단위 'm'를 빼고 숫자만으로 계산해봐요.

먼저 밑변에 해당하는 건물에서 운동장까지의 길이 50을 거듭 곱하면 '2500'이 나오죠. 그리고 건물 높이 10을 두번 곱하면 '100'이 나옵니다. 피타고라스 정리에 따르면, 이 둘을 더한 것이 옥상에서 운동장까지 길이를 거듭 곱한 것과 같아야겠지요. 정말 그런지 볼까요? 옥상에서 운동장까지 매달 만국기 길이 51을 두번 곱하니 '2601'이 나왔어요. 우와, 오히려 1m가 남네요. 건물 옥상에서 운동장까지 넉넉히 연결할 수 있겠군요. 이제 선생님이 만국기를 문제 없이 매달 수 있었던 비결을 알겠지요?